二维绕原点旋转矩阵
# 前言
公司有个需求需要计算图片旋转任意角度后的包围框坐标，这就需要用到旋转矩阵，虽然百度可以很容易的搜索到，但是我这个人喜欢刨根问底然后举一反三，不懂原理心里就痒痒。所以就从矩阵开始学起。
# 矩阵的数学定义
矩阵在3D数学中具有根本意义上的重要性，它们主要用于描述两个坐标空间之间的关系。它们通过定义矢量从一个坐标空间转换为另一个坐标空间来实现目的。
在线性代数中，矩阵是排列成行和列的矩形数字网格。
# 矩阵维度和表示法
对于具有r行和c列的矩阵，称为是r×c（读作r乘c）矩阵。例如，一下一个4 × 3矩阵有4行3列：
当希望引用矩阵中的各个元素时，将使用下标表示法，通常用相应的小写斜体字母。例如，一下就是一个3×3矩阵：
符号mij表示矩阵M的行i列j中的元素
# 方形矩阵
具有相同行数和列数的矩阵称为方形矩阵（Square Matrice），并且它是特别重要的内容。
方形矩阵的对角元素（Diagonal Elements）是行和列索引相同的元素。例如，3×3矩阵M的对角元素是m11、m22和m33。
如果矩阵中的所有非对角元素都为0，则该矩阵为对角矩阵（Diagonal Matrix）。以下4×4矩阵就是一个对角矩阵：
有一类特殊的对角矩阵是单位矩阵（Identity Matrix）。维度为n的单位矩阵，表示为In,是n×n矩阵，其对角线上的值为1，其他元素均为0。例如，以下是一个3×3单位矩阵：
# 作为矩阵的矢量
矩阵可以包含任何正数的行和列，包括一个。
维数n的矢量可以被视为 1×n 矩阵，或者被视为n×1矩阵。
1×n矩阵称为行矢量，n×1矩阵称为列矢量。行矢量以横向方式书写，列矢量则以纵向方式书写：
注意
当使用带有矩阵的矢量时，必须非常清楚该矢量是行矢量还是列矢量。
# 矩阵转置
给定 r × c矩阵M，M的转置表示为MT,是c×r矩阵，其中，列由M的行构成。这实际上是以对角方式翻转矩阵。
对于矢量，转置会将行矢量转换为列矢量
反之亦然。
注意
- 对于任何维度的矩阵M，（MT）T = M。换句话说，如果先转置矩阵，然后再转置一次，即可得到原始矩阵。此规则也适用于矢量。
- 任何对角矩阵D等于其转置：DT = D。包括单位矩阵I也是如此
# 矩阵与标量相乘
矩阵M可以与标量k相乘，得到与M相同维度的矩阵。我们通过将标量和矩阵并排放置（通常标量在左边）来表示标量与矩阵的乘法。中间不需要乘法符号。
结果矩阵kM中的每个元素是k与M中相应元素的乘积。
# 两个矩阵相乘
某些情况下，可以采用两个矩阵的乘积。当允许矩阵乘法时，其结果的计算规则乍看之下可能有点奇怪。
一个r×n矩阵A可以乘以一个n×c矩阵B。其结果（以AB表示）是一个r×c矩阵。
例如：A是一个4×2矩阵，B是一个2×5矩阵，那么AB将是一个4×5矩阵。
注意
如果A中的列数与B中的行数不匹配，则乘法结果AB未定义（尽管BA是有可能的）
矩阵乘法计算如下：
设矩阵C为 r×n矩阵A 与 n×c矩阵B的 r×c乘积AB。然后每个元素cij等于A的行i与B的列j的矢量点积，其计算公式为：
这看起来很复杂，但有一个简单的模式：
- 对于结果中的每个元素cij，找到A中的第i行和B中的第j列
- 将行和列的相应元素相乘，并对积求和
cij等于此总和，它相当于A中第i行和B中的第j列的点积
例如 2 × 2 矩阵乘法：
矩阵乘法的注意事项
将任何矩阵M乘以一个方形矩阵S(S放在哪边都可以，即MS或SM都行)，得到与M大小相同的矩阵
大小相同的矩阵，条件是矩阵的大小允许乘法。如果S是单位矩阵I，则结果是原始矩阵M。
MI = IM = M
这就是它被称为单位矩阵的原因！矩阵乘法是不可交换的，一般来说， AB ≠ BA
矩阵乘法是可结合的：
(AB)C = A(BC)
当然，这里假设ABC的大小允许乘法矩阵乘法还可以与标量或矢量乘法结合
(kA)B = k(AB) = A(kB)
(vA)B = v(AB)转置两个矩阵的乘积与以相反顺序取得其转置的乘积相同
(AB)T = BTAT
# 矢量和矩阵相乘
矢量可以被认为是具有一行或一列的矩阵，因此可以用矩阵乘法的规则将矢量和矩阵相乘。现在，我们是使用行矢量还是列矢量就变得非常重要。
不难发现，当将左侧的行矢量乘以右侧的矩阵时，其结果是行矢量；当将坐标的矩阵乘以右边的列矢量时，其结果是列矢量。
提示
结果矢量中的每个元素是原始矢量与矩阵中的单个行或列的点积
矩阵中的每个元素确定输入矢量中的特定元素对输出矢量中的元素有多大“权重”。例如，当使用行矢量时，m12控制输入的x值有多少输出到了y值 。
矢量与矩阵乘法分部在矢量加法上，即对于矢量v、w和矩阵M，有
(v + w)M = vM + wM乘法的结果是矩阵的行或列的线性组合。
# 行与列矢量
当左侧的行矢量与右侧的矩阵相乘时，得到的是以下行矢量：
当右侧的列矢量乘以左侧的矩阵时，得到的是以下列矢量结果
如果忽略它们一个是行矢量而另一个是列矢量的事实会发现，矢量分量的值是不一样的。这就是行矢量和列矢量之间的区别如此重要的原因。
尽管视频游戏编程中的某些矩阵确实表示任意方程组，但是更多的情形是我们所描述的类型的变换矩阵，它表示坐标空间之间的关系。
出于这个目的，行矢量更适合此用法，即转换的顺序从左到右读起来就像一个句子。当发生多个转换时，这一点尤为重要。
例如，如果希望按顺序通过矩阵A、B、C转换矢量v,可以写为vABC,矩阵按照从左到右的变换顺序列出。如果使用列矢量，则矢量位于右侧，因此换换将按从右到左的顺序进行，这种情况下，会写为CBAv。
注意
许多图形书籍和应用程序编程接口都使用行矢量，但是！其他API，例如WebGL使用的是列矢量！所以在使用别人的源码和公式时要非常小心，必须确定知道它采用的是行矢量还是列矢量。
# 矩阵的几何解释
一般来说，方形矩阵可以描述任何线性变换，线性变换将保留直线和平行线，且并没有平移。 但是，几何的其他属性（如长度、角度、面积和体积）可能会因为变换而发生改变。线性变换可以“拉伸”坐标空间，但它不会“弯曲”或“扭曲”它。
我们已经说过，矩阵表示坐标空间变换。因此，当对矩阵进行可视化时，实际上就是在可视化空间变换，即进入新的坐标系。
但是这种变换时什么样的呢？特定三维变换与3×3矩阵内的9个数字之间的关系是什么呢？如何构造一个矩阵来执行一个给定的变换？
为了回答这个问题，让我们看一看，以下当标准基矢量 i=[1,0,0],j=[0,1,0],k=[0,0,1]乘以任意矩阵M时会发生什么？
一旦知道这些基础矢量发生了什么，就知道变换的一切！这是因为任何矢量都可以写成标准基矢量的线性组合，如
v = vxi + vyj + vzk
使用该表达式乘以右侧的矩阵，则可以获得
vM = (vxi + vyj + vzk)M
= (vxi)M + (vyj)M + (vzk)M
= vx(iM) + vy(jM) + vz(kM)
= vx[m11 m12 m13] + vy[m21 m22 m23] + vz[m31 m32 m33]
矢量×矩阵乘法的结果是矩阵行的线性组合。关键是将那些行矢量解释为基矢量。
我们引入约定，使用符号p、q、r来引用一组基矢量。将这些矢量作为行放入矩阵M中，这样就可以将式子重写为
# 应用
现在有一种简单的方法来获取任意矩阵并可视化矩阵所代表的变换类型。
先看个例子：看一下以下的2×2矩阵：
这个矩阵代表什么样的变换呢？
首先，我们从矩阵的行中提取基矢量p和q：
p = [2 1]
q = [-1 2]
下图显示了笛卡尔平面中的这些矢量，以及供参考的“原始”基矢量（也就是x轴和y轴）
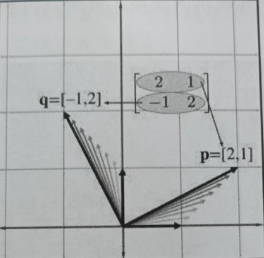
图中，将+x基矢量变换为上面标记为p的矢量，并将+y基矢量标记为q的矢量。
因此，在二维中可视化矩阵的一种方法是可视化由行矢量形成的L形状。在本例中可以很容易看到，由矩阵M表示的变换的一部分是大约26.5°的逆时针旋转的。
当然，所有矢量都受到线性变换的影响，而不仅仅是基矢量。我们可以从L形中很好地了解这种变换的样子，通过完成由基矢量形成的二维平行四边形，可以进一步了解变换对其余矢量的影响。
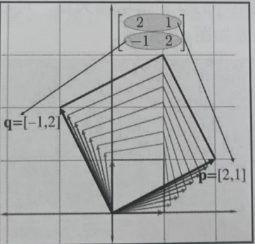
图中形成的这个二维平行四边形也称为倾斜框。在框内绘制一个对象也有助于可视化变换。
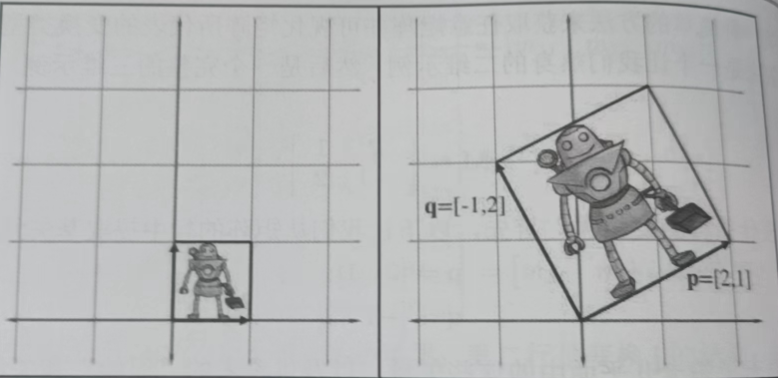现在很明显，示例矩阵M不仅可以旋转坐标空间，还可以对其进行缩放。
# 旋转矩阵
学了这么久的矩阵，终于绕回旋转矩阵本身了。
在二维中，我们实际上只能进行一种旋转：围绕一个点旋转。围绕原点的二维旋转仅具有一个参数，即角度θ，它将定义旋转量。
大多数数学书籍中的标准惯例是考虑逆时针旋转正向和顺时针旋转负向，下图显示了基矢量p和q如何围绕原点旋转，从而产生新的基矢量p'和q'
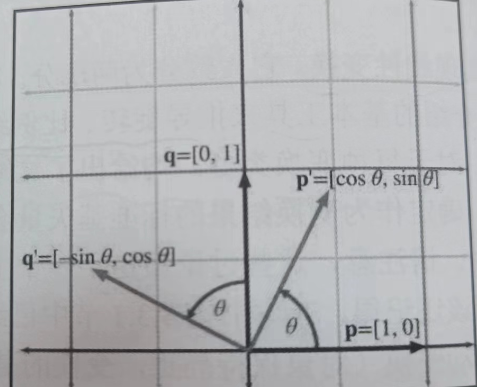
现在我们知道旋转后基矢量的值，即可构建以下二维旋转矩阵：
例：计算坐标点[5, 4]旋转45度后的新坐标点：
# 线性代数的宏大图景
线性代数被发明用于操纵和求解线性方程。例如，传统线性代数课程中的典型入门问题是求解以下形式的方程组：
-5x1 + x2 + x3 = -10
2x1 + 2x2 + 4x3 = 12
x1 - 3x3 = 9
它的解是
x1 = 3
x2 = 7
x3 = -2
发明矩阵表示法是为了避免枯燥地重复写每个x和每个=。例如，上面的方程组和求解结果可以更快地编写为以下形式：
在视频游戏中，也许必须求解大型方程组的最直接和最明显的地方是物理引擎。强制非穿透并满足用户请求的约束称为一个与动态物体的速度相关的方程组。然后，在每个模拟帧中解析该大型系统。
传统的线性代数方法出现的另一个常见的地方是最小二乘近似和其他数据拟合应用。
方程组可以出现在你不期望他们出现的地方。实际上，随着近半个世纪计算能力的大幅增加，线性代数的重要性日益凸显，因为先前既不是离散也不是线性的许多困难问题都是通过两种方法来近似的，例如有限元方法。
这种挑战发轫于知道如何将原始问题转化为矩阵问题，但最终的系统通常非常大，很难快速准确地解决。数值稳定性成为算法选择的一个因素。在实践中出现的矩阵不是充满了随机数字的盒子，相反，它们表达有组织的关系并有很多结构。巧妙的利用这种结构是实现速度和准确性的关键。
线性代数中有一个更宏大的世界。虽然传统的线性代数和方程组在基本视频游戏编程中不起作用，但，它们对许多高级领域而言都是必不可少的。比如流体，布料和头发模拟及渲染；更强大的任务过程动画；实时全局照明；机器视觉；手势识别等。这些看似五花八门的技术都有一个共同点，那就是他们都涉及困难的线性代数问题。
要学习和理解线性代数和科学计算的宏大图景，可以去ocw.mit.edu的MIT OpenCourseWare去看Gilbert Strang教授的系列讲座。
# 后记
知识是所有一切的根，是基石，我也想不带任何功利心慢慢的学习，愿自己往后的岁月能坚守自己的初心，坚定的走在自己的道路上。