判断路径是顺时针还是逆时针
更新时间: 2024-04-15 09:25:09
# 矢量叉积
首先需要先学一样东西,叫做矢量叉积
现有 矢量a = (x1, y1),矢量b = (x2, y2), a × b = (x1y2 - x2y1),方向垂直于原始的两个矢量。
我们已经说过 a × b 垂直于 a 和 b,但又两个垂直于 a 和 b 的方向,具体垂直指向哪边呢?这个符合右手定则:
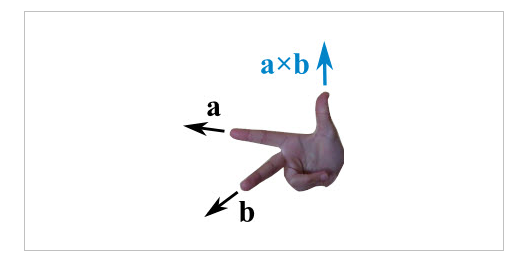
把食指指向矢量a的方向,把中指指向矢量b的方向,拇指指着的方向就是叉积的方向。
# 算法设计
我们可以在路径上找出三个点来构成两个矢量,再使用叉积公式判断叉积是正还是负:
- 如果叉积小于0, 则为顺时针
- 如果叉积大于0,则为逆时针
- 如果叉积等于0, 则平行
当多边形是凸多边形时,各个点均满足这个规律,但如果是凹多边形,再凹边处就会存在特殊情况。
因此,我们需要找到一个绝对为凸边的点,我们找到路径中x最大的点,这个点一定会是凸边,通过这个点与相邻的两个点构成的矢量就可以通过叉积知道路径的走向了。
// 判断路径是否为顺时针方向,顺时针范围true, 逆时针为false
function isClockwise(points) {
// 找到x最大的点的index
var maxXIndex = 0;
var maxX = points[maxXIndex][0];
var c1,c2,c3;
var x1,y1,x2,y2,x3,y3;
for(var i=0;i<points.length;i++){
if(points[i][0]>maxX){
maxX = points[i][0]
maxXIndex = i;
}
}
if(maxXIndex==0){
// 如果是第1个点x最大,那另外两个点为路径最后一个点和第二个点
c1 = points[points.length-1];
c2 = points[maxXIndex];
c3 = points[maxXIndex+1];
}else if(maxXIndex==points.length-1){
// 如果是最后一个点x最大,另外两个点为倒数第二个点和第一个点
c1 = points[maxXIndex-1];
c2 = points[maxXIndex];
c3 = points[0];
}else {
// 如果不是第1和最后一个点x最大,那另外两个点就是正常的前一个和后一个点
c1 = points[maxXIndex-1];
c2 = points[maxXIndex];
c3 = points[maxXIndex+1];
}
x1 = c1[0];
y1 = c1[1];
x2 = c2[0];
y2 = c2[1];
x3 = c3[0];
y3 = c3[1];
// - 如果叉积小于0, 则为顺时针
// - 如果叉积大于0,则为逆时针
// - 如果叉积等于0, 则平行
var s = ((x1-x3)*(y2-y3)-(x2-x3)*(y1-y3));
return s<0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
